You’ve heard that neural networks power everything from face recognition to language models. They’re behind the AI revolution transforming technology. But what exactly is a neural network, and how does it actually work?
Most explanations dive into complex mathematics or use confusing jargon that leaves you more confused than when you started. Understanding neural networks doesn’t require a PhD, and learning how these systems work opens the door to deep learning. Let me break down neural networks in a way that actually makes sense.
A neural network is a machine learning model inspired by how biological brains process information. It consists of layers of artificial neurons that work together to transform input data into useful outputs. Think of it as a sophisticated pattern recognition system that learns from examples rather than following pre-programmed rules.
From biological brains to artificial neurons
Your brain contains roughly 86 billion neurons connected through trillions of synapses. Each neuron receives signals from other neurons, processes them, and sends signals to more neurons. This massive network of simple processing units creates intelligence through their collective behavior.
Artificial neural networks borrow this basic concept but simplify it dramatically. An artificial neuron is a mathematical function that takes multiple inputs, combines them with weights, and produces an output. It’s nowhere near as complex as a biological neuron, but the principle is similar.
A biological neuron fires when the combined strength of incoming signals exceeds some threshold. An artificial neuron does something similar. It calculates a weighted sum of its inputs, adds a bias term, then applies an activation function to produce its output.
The math looks like this: take each input value, multiply it by a weight, add them all together, add a bias, then apply an activation function. The weights determine how important each input is. The bias shifts the activation threshold. The activation function introduces non-linearity.
Don’t worry if that sounds abstract. A concrete example makes it clear. Suppose you’re deciding whether to go running. You consider temperature, available time, and energy level. Each factor has different importance to you. Temperature might matter a lot, time somewhat, energy a bit. An artificial neuron works the same way, mathematically combining factors with learned importance weights.
How neural network layers work together
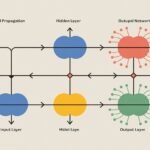
A single neuron can only learn simple patterns. The power comes from connecting many neurons in layers. A typical neural network has an input layer, one or more hidden layers, and an output layer.
The input layer receives your raw data. If you’re classifying images, each pixel becomes an input neuron. If you’re predicting house prices, features like square footage and bedrooms become inputs. The input layer just passes data forward without transformation.
Hidden layers do the actual learning and pattern recognition. Each hidden layer neuron receives inputs from the previous layer, applies its weights and activation function, and sends output to the next layer. Early layers might detect simple patterns. Later layers combine those into more complex patterns.
The output layer produces your final prediction. For classification with two categories, you might have one output neuron. For multi-class classification, you have one output neuron per class. For regression predicting a number, you typically have one output neuron.
import numpy as np
# Simple neural network structure
input_layer = np.array([1.5, 2.0, 0.5]) # 3 input features
hidden_layer_weights = np.array([
[0.2, 0.8, 0.5],
[0.7, 0.1, 0.9]
]) # 2 hidden neurons, each with 3 weights
# Calculate hidden layer outputs
hidden_outputs = []
for neuron_weights in hidden_layer_weights:
weighted_sum = np.dot(input_layer, neuron_weights)
# Apply activation (ReLU: max(0, x))
output = max(0, weighted_sum)
hidden_outputs.append(output)
print(f"Hidden layer outputs: {hidden_outputs}")
This code shows a simple network with 3 inputs and 2 hidden neurons. Each hidden neuron calculates a weighted sum of inputs then applies an activation function. The outputs become inputs to the next layer.
Activation functions bring non-linearity
Without activation functions, stacking layers would be pointless. Multiple linear transformations combined just create another linear transformation. You could replace the entire network with a single layer doing the same thing.
Activation functions introduce non-linearity, letting networks learn complex curved patterns rather than just straight lines. Several activation functions are commonly used.
ReLU or rectified linear unit is the most popular. It outputs the input if positive, otherwise outputs zero. Mathematically it’s max(0, x). ReLU is simple, fast to compute, and works well in practice. It prevents the vanishing gradient problem that plagued earlier networks.
Sigmoid squashes inputs to a range between 0 and 1. It’s useful for output layers when you want probabilities. The S-shaped curve smoothly transitions from 0 to 1. However, sigmoid can cause vanishing gradients in deep networks, so it’s rarely used in hidden layers anymore.
Tanh is similar to sigmoid but outputs values between negative 1 and 1. It’s centered at zero which can help learning. Like sigmoid, it’s mostly replaced by ReLU for hidden layers.
Softmax is used in output layers for multi-class classification. It converts a vector of numbers into probabilities that sum to 1. Each output represents the probability of one class.
# Common activation functions
def relu(x):
return max(0, x)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def tanh(x):
return np.tanh(x)
# Example activations
x = 2.0
print(f"ReLU({x}) = {relu(x)}")
print(f"Sigmoid({x}) = {sigmoid(x):.4f}")
print(f"Tanh({x}) = {tanh(x):.4f}")
The choice of activation function affects how well and how fast your network learns. ReLU is the default choice for hidden layers. Sigmoid works for binary classification outputs. Softmax works for multi-class classification outputs.
Weights, biases, and learning
When you create a neural network, the weights and biases start with random values. The network makes terrible predictions because it hasn’t learned anything yet. Training adjusts these parameters so the network makes better predictions.
Weights control the strength of connections between neurons. A large positive weight means that input strongly influences the neuron’s output. A large negative weight means the input suppresses the output. A weight near zero means the input barely matters.
Biases shift the activation threshold. They let neurons activate even when weighted inputs sum to zero. Without biases, a neuron receiving all zero inputs would always output zero regardless of its purpose.
Learning happens through a process called backpropagation combined with gradient descent. The network makes predictions, calculates how wrong they are using a loss function, then adjusts weights and biases to reduce that error. This process repeats thousands of times until the network learns useful patterns.
The learning rate controls how much weights change in each update. Too large and training becomes unstable. Too small and training takes forever. Finding the right learning rate is crucial for effective training.
When to use neural networks
Neural networks excel at certain types of problems but aren’t always the best choice. They work brilliantly for image recognition, speech processing, natural language understanding, and other tasks with complex non-linear patterns.
Use neural networks when you have lots of training data and computational resources. They need thousands or millions of examples to learn effectively. They also require significant computing power, especially for training.
Don’t use neural networks when you have small datasets or need interpretability. Traditional machine learning algorithms like random forests often work better with limited data. Decision trees show you exactly how they make decisions while neural networks are black boxes.
Neural networks shine when the relationship between inputs and outputs is complex and non-linear. If a simple linear model or decision tree works well, stick with those simpler approaches. Use neural networks when simpler models fail to capture the patterns in your data.
Modern frameworks like TensorFlow and PyTorch make building neural networks straightforward. You define the architecture, specify the loss function and optimizer, then train on your data. The frameworks handle the complex mathematics automatically.
# Simple neural network with Keras
from tensorflow import keras
from tensorflow.keras import layers
# Define network architecture
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=(10,)),
layers.Dense(32, activation='relu'),
layers.Dense(1, activation='sigmoid')
])
# Compile model
model.compile(
optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy']
)
print(model.summary())
This code creates a neural network with 10 inputs, two hidden layers with 64 and 32 neurons, and one output for binary classification. The framework handles all the mathematical details of forward propagation and backpropagation.
Moving forward with neural networks
What is a neural network becomes clear when you understand the components. Artificial neurons combine inputs with learned weights. Activation functions introduce non-linearity. Layers stack to build complexity. Training adjusts parameters to minimize prediction errors.
The fundamental architecture hasn’t changed much since the 1980s. What changed is having more data, more computing power, and better training techniques. These advances let us build deeper networks that learn more complex patterns.
Neural networks form the foundation of modern deep learning. Convolutional neural networks excel at computer vision. Recurrent neural networks handle sequential data. Transformers power large language models. All build on these basic principles of connected artificial neurons learning from data.
Understanding what neural networks are and how they work prepares you for everything that comes next in deep learning. The concepts of layers, weights, activations, and learning through backpropagation apply to every neural network architecture.
Ready to see how neural networks actually process data from input to output? Check out our guide on forward propagation explained to understand the exact mathematical steps that transform your input into predictions through each layer of the network.